Fast Bit Flag Boolean Expressions

Recently I've been working on a new theming engine for my music app Cantabile and ran across the need for an algorithm that I've not seen discussed in computer science circles before.

The theming engine is built around a custom language called GTL (GuiKit Theming Language) that has a feature where different visual representations for a UI element can be specified based on the current state of that element.

For example, you can specify different colors for a control based on the control's current state:

BackgroundColor:
{
    Checked|Pressed: Color.Blue,
    Checked: Color.LightBlue,
    Else: Color.Black,
}

Currently GTL expects these states to be specified as a bitmask and evaluates them to true when (ControlState & BitMask) == BitMask. This is fine for many cases but is limited in that you can only specify a set of bits that must be set. What if I want to test that one of two bits are set, or that a bit isn't set?

What's really needed here are boolean expressions, or more specifically "Bit Flag Boolean Expressions".  That is, expressions that use typical C style boolean operators ( && , || , and ! ), but work on the individual bits in an input word.

• Checked && Pressed
• Focused && !Disabled
• Focused || Selected

Besides being more flexible in the types of conditions that can be expressed, boolean expressions are also a more intuitive way to express these conditions. eg: Checked | Pressed reads as "checked or pressed", but the condition we're actually trying to describe is "checked and pressed".

While it's pretty easy to parse and evaluate a boolean expression walking and evaluating an expression tree is going to be slower than a simple bit mask and test where multiple boolean operations can often be reduced to a single operation.

But what if we could convert the expression tree to a series of bit mask and test operations automatically? So, the question is:

How do we convert an abstract syntax tree for a boolean expression into an optimal set of mask and test operations?

I posted the question to StackOverflow, but ended up finding a good solution myself and thought it was worth writing up.

Tokenizing and Parsing

I've written about tokenizing and parsing expressions into abstract syntax trees before so I won't cover it again here.  If this is new to you, see this article.

For this algorithm to work properly the AST needs to represent boolean AND and OR operators as multi-input nodes rather than a chain of binary nodes as is often seen in expression syntax trees.

Since these operations are commutative (ie: can be evaluated in any order) making them all inputs to a single node provides more opportunities to re-order and coalesce boolean operations into a wider bitmask operation.

For an existing AST/parser implementation this might involve:

1. Updating the AST nodes for boolean AND and OR to accept multiple inputs
2. Updating the parser to parse chains of AND and OR operations into a single node
3. Updating the parser to simplify the AST so that it promotes nodes of the same type into their parent node.  eg: most parsers would produce two binary AND nodes for this expression: A && (B && C) but ideally this should be flattened to one three input node: A && B && C.

The Algorithm

Now that we've got an AST tree in suitable format, lets think about the algorithm. Most of these boolean operations can be reduced to one of two forms of bitmask operations:

• (input & mask) == testValue
• (input & mask) != testValue

The first form which I call MaskEqual is used for boolean AND operations. eg: the boolean expression A && B && !C becomes (input & (A|B|C)) == (A|B)

The second form which I call MaskNotEqual is used for boolean OR operations. eg: the boolean expression A || B || C becomes (input & (A|B|C)) != 0.

Note: throughout this article and in the code base I use the single capital letter symbols such that A = 0x01, B = 0x02, C = 0x04 etc...  So A && B && !C can also be expressed in bitwise form as (input & 0x07) == 0x03.

Next we have expressions that always evaluate to true or false:

• A && !A is always false
• A || !A is always true

And finally, we have expressions that can't be reduced to a single bitwise operation.  eg:  the best we can do with this:

A && (B || C)

is this:

((input & 0x1) == 0x1) && ((input & 0x6) != 0x0)

For those cases we have EvalAnd, EvalOr and EvalNot.

Based on the above we need to calculate an execution plan for every node in the tree where each plan will be one of the following types:

enum ExecPlanKind
{
    True,
    False,
    MaskEqual,
    MaskNotEqual,
    EvalAnd,
    EvalOr,
    EvalNot,
}

Each execution plan node will also have additional data depending on its type:

• True / False - no other data
• MaskEqual / MaskNoteEqual - an associated mask and test value
• EvalAnd / EvalOr / EvalNot - a set of input execution plan nodes

The goal of the algorithm is walk the AST and build a tree of execution plan nodes that minimizes the number of EvalAnd, EvalOr and EvalNot operations - since these require extra steps to execute.

One thing to note about the MaskEqual and MaskNotEqual execution plans is that if the mask has only a single bit set then it's possible to switch the plan from one kind to another by flipping the unmasked bits in the test value and changing the plan kind.

eg: (value & 0x01) == 0x01 is the same as (value & 0x01) != 0x00.

If more that one mask bit is set then the plan can't be converted to the other kind.

Next, let's think about how to translate each node in the AST into an execution plan node.

The Identifier Node

The identifier node represents a name in the expression (eg: A, B, C etc...) and has an associated bit that it represents in the input value.  The execution plan for this kind of node is trivial:

• Kind:ExecPlanKind.MaskEqual
• Mask: the identifier bit value
• TestValue: the identifier bit value

In other words, the expression A which has an bitmask value of 0x01 can be evaluated as (input & 0x01) == 0x01.

The Not Operator

The Not operator has a single input node.  To generate an execution plan, first we calculate the execution plan for the input node and depending on its ExecPlanKind we create a new execution plan that inverts it.

• ExecPlanKind.True => ExecPlanKind.False
• ExecPlanKind.False => ExecPlanKind.True
• ExecPlanKind.MaskEqual => ExecPlanKind.MaskNotEqual (keeping the same mask and value)
• ExecPlanKind.MaskNotEqual => ExecPlanKind.MaskEqual (keeping the same mask and value)
• Otherwise ExecPlanKind.EvalNot, with the input plan of the input operand as the argument

The And and Or Operators

The And and Or operators are the most complex, but very similar to each other.

Here's the logic for the And operator:

1. Calculate the execution plan for each of the inputs and place them in a collection.
2. If any of the input plans are ExecPlanKind.False then regardless of the other inputs the result is also ExecPlanKind.False.
3. If all of the input plans are ExecPlanKind.True the the result is also ExecPlanKind.True.
4. Remove any nodes from the collection that are ExecPlanKind.True since they don't contribute anything to the result.
5. Where possible, convert input plans of type ExecPlanKind.MaskNotEqual to ExecPlanKind.MaskEqual. Without this conversion, expressions like A && B && !C can't be reduced because of the way the Not operator works. (see the note above about only converting these when a single bit is set).
6. Coalesce all ExecPlanKind.MaskEqual input plans into a single MaskEqual plan that Or's the input masks and test values together.  The only catch here is to detect cases where the there's a conflicting test value bit for any of the masked bits.  Such a case will always be false (eg: A && !A) and if detected the execution plan for this node becomes just ExecPlanKind.False.
7. After applying the above steps if there's only one input plan left in the collection then that plan becomes the plan for this node.
8. Otherwise, there are multiple input plans left in the collection and they need to be evaluated sequentially at runtime. The plan for this node becomes ExecPlanKind.EvalAnd with the current collection of input plans as its input.

As mentioned the Or operator is basically the same with some of the logic flipped - see the source code for details.

Executing the Execution Plan

The output of the above algorithm is an execution plan and to execute it we just need an input value to test against:

public bool Evaluate(ulong input)
{
    switch (Kind)
    {
        case ExecPlanKind.True: 
            return true;

        case ExecPlanKind.False: 
            return false;

        case ExecPlanKind.MaskEqual: 
            return (input & Mask) == TestValue;

        case ExecPlanKind.MaskNotEqual: 
            return (input & Mask) != TestValue;

        case ExecPlanKind.EvalAnd: 
            return InputPlans.All(x => x.Evaluate(input));

        case ExecPlanKind.EvalOr: 
            return InputPlans.Any(x => x.Evaluate(input));

        case ExecPlanKind.EvalNot: 
            return !InputPlans[0].Evaluate(input);
    }
}

Testing and Results

To verify the results of the optimized execution plan, an expression evaluator that works directly using the AST was also implemented and the results compared with the optimized plan over a range of inputs and against a representative set of expressions

To get an idea of the kinds of operations that are generated by this algorithm, the sample program displays the boolean expression and its equivalent bitmask expression:

A && !A  =>  false
A || !A  =>  true
A  =>  (input & 0x1) == 0x1
B  =>  (input & 0x2) == 0x2
C  =>  (input & 0x4) == 0x4
D  =>  (input & 0x8) == 0x8
A && B  =>  (input & 0x3) == 0x3
A || B  =>  (input & 0x3) != 0x0
A && (B || C)  =>  ((input & 0x1) == 0x1) && ((input & 0x6) != 0x0)
(A && B) || C  =>  ((input & 0x4) != 0x0) || ((input & 0x3) == 0x3)
(A && B) || (C && D)  =>  ((input & 0x3) == 0x3) || ((input & 0xC) == 0xC)
(A || B) && (C || D)  =>  ((input & 0x3) != 0x0) && ((input & 0xC) != 0x0)
(A || B) && (C || D) && (A || C) && (A || D)  =>  ((input & 0x3) != 0x0) && ((input & 0xC) != 0x0) && ((input & 0x5) != 0x0) && ((input & 0x9) != 0x0)

But what about performance?  On the above set of expressions the optimized execution plans ran on average more than 60% faster that the non-optimized version. (approx 2.9 down to 1.1 seconds)

More Performance with ILGenerator

I really wanted to squeeze as much performance as I could out of these expressions since the UI library calls them fairly regularly during rendering and control state updates.

One of the coolest features of .NET are dynamic methods - the ability to generate IL code at runtime that effectively gets compiled to machine code.

Given the optimized execution plans from above it's really quite simple to generate IL code to actually execute them.  Here's the entire function that generates the IL for an execution plan:

void Emit(ExecPlan plan)
{
    switch (plan.Kind)
    {
        case ExecPlanKind.True:
            _il.Emit(OpCodes.Ldc_I4_1);
            break;

        case ExecPlanKind.False:
            _il.Emit(OpCodes.Ldc_I4_0);
            break;

        case ExecPlanKind.MaskEqual:
            _il.Emit(OpCodes.Ldarg_0);
            _il.Emit(OpCodes.Ldc_I4, plan.Mask);
            _il.Emit(OpCodes.And);
            _il.Emit(OpCodes.Ldc_I4, plan.TestValue);
            _il.Emit(OpCodes.Ceq);
            break;

        case ExecPlanKind.MaskNotEqual:
            _il.Emit(OpCodes.Ldarg_0);
            _il.Emit(OpCodes.Ldc_I4, plan.Mask);
            _il.Emit(OpCodes.And);
            _il.Emit(OpCodes.Ldc_I4, plan.TestValue);
            _il.Emit(OpCodes.Ceq);
            _il.Emit(OpCodes.Ldc_I4_0);
            _il.Emit(OpCodes.Ceq);
            break;

        case ExecPlanKind.EvalAnd:
            {
                var lblFalse = _il.DefineLabel();
                var lblDone = _il.DefineLabel();
                for (int i = 0; i < plan.InputPlans.Count; i++)
                {
                    // Generate the input plan
                    Emit(plan.InputPlans[i]);
                    _il.Emit(OpCodes.Brfalse, lblFalse);
                }
                _il.Emit(OpCodes.Ldc_I4_1);
                _il.Emit(OpCodes.Br_S, lblDone);
                _il.MarkLabel(lblFalse);
                _il.Emit(OpCodes.Ldc_I4_0);
                _il.MarkLabel(lblDone);
                return;
            }

        case ExecPlanKind.EvalOr:
            {
                var lblTrue = _il.DefineLabel();
                var lblDone = _il.DefineLabel();
                for (int i = 0; i < plan.InputPlans.Count; i++)
                {
                    // Generate the input plan
                    Emit(plan.InputPlans[i]);
                    _il.Emit(OpCodes.Brtrue, lblTrue);
                }
                _il.Emit(OpCodes.Ldc_I4_0);
                _il.Emit(OpCodes.Br_S, lblDone);
                _il.MarkLabel(lblTrue);
                _il.Emit(OpCodes.Ldc_I4_1);
                _il.MarkLabel(lblDone);
                break;
            }

        case ExecPlanKind.EvalNot:
            {
                Emit(plan.InputPlans[0]);
                _il.Emit(OpCodes.Ldc_I4_0);
                _il.Emit(OpCodes.Ceq);
                break;
            }

        default:
            throw new NotImplementedException();
    }
}

Using the above approach, performance jumped to almost 90% faster than directly evaluating the unoptimized tree.  (approx 2.9 down to 0.4 seconds). Well worth the effort!

About the Code

The code for this is available here.  Some notes:

• A Visitor Pattern is used for walking the AST
• It should probably use the Visitor pattern for ExecPlan nodes too (but it doesn't)
• Most of the logic can be found where you'd expect - the Tokenizer is in Tokenizer.cs, the Parser in Parser.cs etc...
• The Evaluator class evaluates an unoptimized AST tree against an input value
• The Planner class produces an optimized ExecPlan from a supplied AST
• The Compiler class generates IL code for a suppliedExecPlan
• The Logger class is used log an expression AST to the console
• All the AST nodes are in AstNodes.cs
• The IBitNames interface allows plugging in a mapping from expression identifier to bit mask
• The BitFromLetter class provides a hardcoded implementation of IBitNames where A = 0x01, B = 0x02, C = 0x04 etc... and is used only for testing.
• The EnumNames class provides an implementation of IBitNames that retrieves bit values from a C# enum type.

Finally, the Compiler class also includes this method:

public static Func<T, bool> Compile<T>(string expression) where T: Enum

It can be used to create an IL optimized method for an expression based on a C# enum:

[Flags]
enum Fruit
{
    Apples = 0x01,
    Pears = 0x02,
    Bananas = 0x04,
}

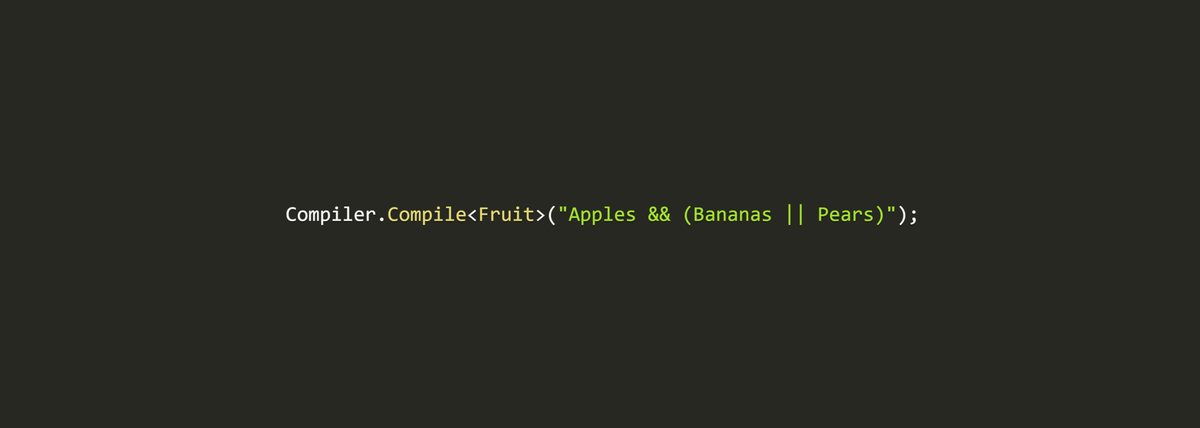
var compiledExpression = Compiler.Compile<Fruit>("Apples && (Bananas || Pears)");
var result = compiledExpression(Fruit.Apples|Fruit.Bananas);

The compiler supports generating IL code for enum types with a 8, 16, 32 and 64-bit underlying types.

Now I just need to retrofit it into GTL.

PS: If you've seen this or a similar algorithm before, I'd be interested in reading about it - let me know.