Writing a Simple Math Expression Engine in C#
This post explains how to build a simple expression engine in C#. It covers topics like tokenizing, parsing, building an expression tree and then evaluating the resulting expression.
If you've never learned about language processing or compilers this is a great introduction and also forms a good starting point for a more comprehensive expression engine.
What is an Expression Engine?
An expression engine is a library that can take a string like the following and calculate a resulting value.
2 * pi * rYou could use this to let a user type math expressions into an input field, or to define custom functions for a graph plotting application for example.
The implementation I describe here will support:
- Numbers only (ie: C#
double) - The basic math operations (add, subtract, multiply, divide)
- Correct order of operation
- Variables
- Functions
- Ability to call C# through reflection
I’ve made the source code for this available and there are branches for each of the seven steps described below. Feel free to do with this code as you wish but note that it’s been written in a manner to best demonstrate the topics at hand — as you extend it you’ll almost certainly find better ways to implement some parts of it.
Many languages have a built-in ability to evaluate expressions in the language’s own syntax (eg: JavaScript’s eval function). The point of this article is not to just provide a way to evaluate an expression — it’s intended to teach how to build an expression engine where a very specific syntax is needed.
This is a fairly fast moving tutorial with lots of code samples but by the end of it you should have a solid understanding of how to build a flexible and powerful expression evaluation engine.
Step 1 — The Tokenizer
The first thing we need to evaluate an expression is a tokenizer. The tokenizer’s job is to break the expression string into a series of tokens where each token describes one piece of the input string.
For example the string “10 + 20” would be tokenized to three tokens:
1. Token Number "10"
2. Token Add
3. Token Number "20"Lets start by defining a Token enumerated type:
public enum Token
{
EOF,
Add,
Subtract,
Number,
}and a Tokenizer class that reads from a TextReader and provides a way to read the current token and move to the next:
public class Tokenizer
{
public Tokenizer(TextReader reader);
// The current token
public Token Token { get; }
// The value of the number of Token.Number
public double Number { get; }
// Move to the next token
public void NextToken() { }
}The implementation of the Tokenizer class is reasonably straight forward — it skips whitespace, looks for special characters and parses numbers into doubles. See full source code here.
The tokenizer is used like so:
var testString = "10 + 20 - 30.123";
var t = new Tokenizer(new StringReader(testString));
// "10"
Assert.AreEqual(t.Token, Token.Number);
Assert.AreEqual(t.Number, 10);
t.NextToken();
// "+"
Assert.AreEqual(t.Token, Token.Add);
t.NextToken();
// etc...Step 2 — The Parser and Add/Subtract
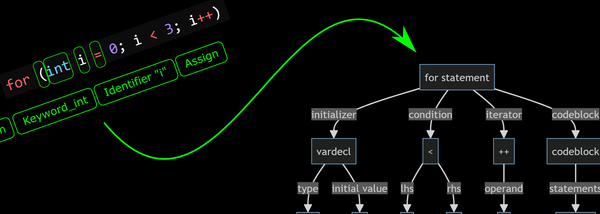
The next step is to read the stream of tokens generated by the tokenizer and generate an expression tree — a hierarchy of nodes that represent the structure of the expression.
For example the expression “10 + 20” would be represented by three nodes:
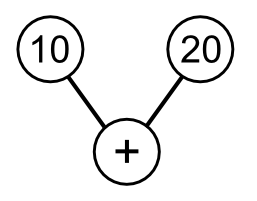
We’ll need a couple of different node types but they’ll all derive from a common base class Node which has a method Eval that returns the node’s value.
The simplest kind of node is a NodeNumber which represents a literal number (ie: the 10 and 20 in the above example).
public abstract class Node
{
public abstract double Eval();
}
class NodeNumber : Node
{
public NodeNumber(double number)
{
_number = number;
}
double _number; // The number
public override double Eval()
{
// Just return it. Too easy.
return _number;
}
}
Add and Subtract are both binary operations — they have two operands and perform some operation on them. Let’s define a node for binary operations:
// NodeBinary for binary operations such as Add, Subtract etc...
class NodeBinary : Node
{
// Constructor accepts the two nodes to be operated on and function
// that performs the actual operation
public NodeBinary(Node lhs, Node rhs, Func<double, double, double> op)
{
_lhs = lhs;
_rhs = rhs;
_op = op;
}
Node _lhs; // Left hand side of the operation
Node _rhs; // Right hand side of the operation
Func<double, double, double> _op; // The callback operator
public override double Eval()
{
// Evaluate both sides
var lhsVal = _lhs.Eval();
var rhsVal = _rhs.Eval();
// Evaluate and return
var result = _op(lhsVal, rhsVal);
return result;
}
}The important things to note about NodeBinary are:
- It takes two other
Node’s as its operands. This is how the expression tree is constructed. - It takes a
Func<>that defines the actual operation - The
Evalfunction first evaluates the two operand nodes and then calls theFunc<>to “do the operation”.
We could now manually construct an expression tree like this:
// Construct an expression tree
var expr = new NodeBinary(
new NodeNumber(10),
new NodeNumber(20),
(a,b) => a + b
);
// Evaluate it
var result = expr.Eval();
// Check
Assert.AreEqual(result, 30);Of course what we really want to do is construct this tree from our stream of tokens. This is the job of the Parser.
I’ve included the entire first version of the Parser class here. Take the time to understand it because it’s the core of the expression engine and everything that follows builds upon it.
- Parser reads tokens from a supplied
Tokenizer - The
ParseLeaf()method creates aNodeNumberif the current token is a number - The
ParseAddSubtractmethod parses a leaf for the left hand side and then checks if it’s followed by an add or subtract token. If it is then it parses another leaf for the right-hand side and joins them with an appropriateNodeBinary. ParseAddSubtractwill handle a sequence of add/subtract operations. (eg: “10 + 20 – 30 + 40” etc…)
public class Parser
{
// Constructor - just store the tokenizer
public Parser(Tokenizer tokenizer)
{
_tokenizer = tokenizer;
}
Tokenizer _tokenizer;
// Parse an entire expression and check EOF was reached
public Node ParseExpression()
{
// For the moment, all we understand is add and subtract
var expr = ParseAddSubtract();
// Check everything was consumed
if (_tokenizer.Token != Token.EOF)
throw new SyntaxException("Unexpected characters at end of expression");
return expr;
}
// Parse an sequence of add/subtract operators
Node ParseAddSubtract()
{
// Parse the left hand side
var lhs = ParseLeaf();
while (true)
{
// Work out the operator
Func<double, double, double> op = null;
if (_tokenizer.Token == Token.Add)
{
op = (a, b) => a + b;
}
else if (_tokenizer.Token == Token.Subtract)
{
op = (a, b) => a - b;
}
// Binary operator found?
if (op == null)
return lhs; // no
// Skip the operator
_tokenizer.NextToken();
// Parse the right hand side of the expression
var rhs = ParseLeaf();
// Create a binary node and use it as the left-hand side from now on
lhs = new NodeBinary(lhs, rhs, op);
}
}
// Parse a leaf node
// (For the moment this is just a number)
Node ParseLeaf()
{
// Is it a number?
if (_tokenizer.Token == Token.Number)
{
var node = new NodeNumber(_tokenizer.Number);
_tokenizer.NextToken();
return node;
}
// Don't Understand
throw new SyntaxException($"Unexpect token: {_tokenizer.Token}");
}
}Parser also includes a couple of static convenience methods (see full code) to automatically create a TextReader and Tokenizer for a string. The following test cases now work:
[TestMethod]
public void AddSubtractTest()
{
// Add
Assert.AreEqual(Parser.Parse("10 + 20").Eval(), 30);
// Subtract
Assert.AreEqual(Parser.Parse("10 - 20").Eval(), -10);
// Sequence
Assert.AreEqual(Parser.Parse("10 + 20 - 40 + 100").Eval(), 90);
}See what just happened? This is now a functioning expression engine that’s actually evaluating expressions. It’s just a little limited.
Part 3 — Unary Operations
One subtle problem with the above is that it doesn’t support negative numbers. eg: this expression would fail with a syntax error:
10 + -20What we need is a “negate” operator. NodeUnary is identical to NodeBinary with one less argument (see here) and can be used for the negate operation.
There’s two interesting aspects to consider here:
- There’s also a “positive” operator. eg: “
10 + +20” is valid - The right hand side of a unary operator can be another unary operator. eg: “
10 + -+20” is also valid. “ten plus negative positive twenty”.
To support this the Parser class has been updated with a new ParseUnary method and ParseAddSubtract is updated to call it instead of ParseLeaf for the left and right hand sides of the operation.
// Parse a unary operator (eg: negative/positive)
Node ParseUnary()
{
// Positive operator is a no-op so just skip it
if (_tokenizer.Token == Token.Add)
{
// Skip
_tokenizer.NextToken();
return ParseUnary();
}
// Negative operator
if (_tokenizer.Token == Token.Subtract)
{
// Skip
_tokenizer.NextToken();
// Parse RHS
// Note this recurses to self to support negative of a negative
var rhs = ParseUnary();
// Create unary node
return new NodeUnary(rhs, (a) => -a);
}
// No positive/negative operator so parse a leaf node
return ParseLeaf();
}Here’s the test cases:
// Negative
Assert.AreEqual(Parser.Parse("-10").Eval(), -10);
// Positive
Assert.AreEqual(Parser.Parse("+10").Eval(), 10);
// Negative of a negative
Assert.AreEqual(Parser.Parse("--10").Eval(), 10);
// Woah!
Assert.AreEqual(Parser.Parse("--++-+-10").Eval(), 10);
// All together now
Assert.AreEqual(Parser.Parse("10 + -20 - +30").Eval(), -40);Part 4 — Multiply, Divide, Parenthesis and Order Of Operation
So far the Parser class has the following methods to generate expression nodes:
ParseAddSubtractParseUnaryParseLeaf
It may not be obvious at first glance but the order these methods call each other determines “order of operation” with lower priority parse methods calling higher priority methods.
Multiply and Divide are higher priority operations than Add and Subtract, but lower than Negate so adding support for Multiply and Divide simply means adding some new tokens, writing a new method ParseMultiplyDivide (exactly like ParseAddSubtract) and sitting it in the call hierarchy between ParseAddSubtract and ParseUnary. ie:
ParseAddSubtractshould callParseMultiplyDividefor its operandsParseMultiplyDivideshould callParseUnaryfor its operands
As an example, consider this expression:
10 + 20 * 30After ParseAddSubtract has parsed the token for add, it calls ParseMultiplyDivide which will consume the “20 * 30” to yield a multiply node which becomes the right hand node for the add operation.
A similar approach is used for parentheses, or bracketed expression:
- Add new tokens for
OpenParensandCloseParensand update the tokenizer to support them - Update
ParseLeafto recognise these tokens and parse the bracketed expression.
Because the bracketed expression is essentially an entire expression in itself it’s parsed using ParseAddSubtract:
// Parenthesis?
if (_tokenizer.Token == Token.OpenParens)
{
// Skip '('
_tokenizer.NextToken();
// Parse a top-level expression
var node = ParseAddSubtract();
// Check and skip ')'
if (_tokenizer.Token != Token.CloseParens)
throw new SyntaxException("Missing close parenthesis");
_tokenizer.NextToken();
// Return
return node;
}The parser now supports the entire expression syntax and correctly handles order of operation:
// No parens
Assert.AreEqual(Parser.Parse("10 + 20 * 30").Eval(), 610);
// Parens
Assert.AreEqual(Parser.Parse("(10 + 20) * 30").Eval(), 900);
// Parens and negative
Assert.AreEqual(Parser.Parse("-(10 + 20) * 30").Eval(), -900);
// Nested
Assert.AreEqual(Parser.Parse("-((10 + 20) * 5) * 30").Eval(), -4500);Part 5 — Variables
So far the expression engine might be handy for letting a user do simple math in a text input field but its limited in that it only supports literal numbers. The next thing to add is variables.
First, the tokenizer needs to be updated to recognize “identifiers”. ie: variable names.
// Identifier - starts with letter or underscore
if (char.IsLetter(_currentChar) || _currentChar == '_')
{
var sb = new StringBuilder();
// Accept letter, digit or underscore
while (char.IsLetterOrDigit(_currentChar) || _currentChar == '_')
{
sb.Append(_currentChar);
NextChar();
}
// Setup token
_identifier = sb.ToString();
_currentToken = Token.Identifier;
return;
}Next there’s a new node class NodeVariable that stores the name of the variable and calls an IContext to get the variable’s value when the expression is evaluated.
IContext provides a way for the expression to call out to external code. The other node types all need to be updated to pass this variable through.
// Expression context
public interface IContext
{
double ResolveVariable(string name);
}
// Represents a variable (or a constant) in an expression. eg: "2 * pi"
public class NodeVariable : Node
{
public NodeVariable(string variableName)
{
_variableName = variableName;
}
string _variableName;
public override double Eval(IContext ctx)
{
return ctx.ResolveVariable(_variableName);
}
}The final step is to update ParseLeaf to generate the new node:
// Variable
if (_tokenizer.Token == Token.Identifier)
{
var node = new NodeVariable(_tokenizer.Identifier);
_tokenizer.NextToken();
return node;
}Here’s a simple example of a context that provides two variables- “pi” and “r”:
class MyContext : IContext
{
public MyContext(double r)
{
_r = r;
}
double _r;
public double ResolveVariable(string name)
{
switch (name)
{
case "pi": return Math.PI;
case "r": return _r;
}
throw new InvalidDataException($"Unknown variable: '{name}'");
}
}
[TestMethod]
public void Variables()
{
var ctx = new MyContext(10);
Assert.AreEqual(Parser.Parse("2 * pi * r").Eval(ctx), 2 * Math.PI * 10);
}Part 6 — Functions
Functions are really just a more advanced version of variables — an identifier followed by a bracketed and comma separated list of arguments expressions.
NodeFunctionCall is just like NodeVariable but in addition to the name of the function it also accepts an array of expression nodes that are the function arguments. Also, IContext is updated with a new method CallFunction.
public interface IContext
{
double ResolveVariable(string name);
double CallFunction(string name, double[] arguments);
}
public class NodeFunctionCall : Node
{
public NodeFunctionCall(string functionName, Node[] arguments)
{
_functionName = functionName;
_arguments = arguments;
}
string _functionName;
Node[] _arguments;
public override double Eval(IContext ctx)
{
// Evaluate all arguments
var argVals = new double[_arguments.Length];
for (int i=0; i<_arguments.Length; i++)
{
argVals[i] = _arguments[i].Eval(ctx);
}
// Call the function
return ctx.CallFunction(_functionName, argVals);
}
}You should be able to guess how the parsing of functions work so I won’t include the code here. (You can find it here).
Here’s how it would be used:
class MyFunctionContext : IContext
{
public MyFunctionContext()
{
}
public double ResolveVariable(string name)
{
throw new InvalidDataException($"Unknown variable: '{name}'");
}
public double CallFunction(string name, double[] arguments)
{
if (name == "rectArea")
{
return arguments[0] * arguments[1];
}
if (name == "rectPerimeter")
{
return (arguments[0] + arguments[1]) * 2;
}
throw new InvalidDataException($"Unknown function: '{name}'");
}
}
[TestMethod]
public void Functions()
{
var ctx = new MyFunctionContext();
Assert.AreEqual(Parser.Parse("rectArea(10,20)").Eval(ctx), 200);
Assert.AreEqual(Parser.Parse("rectPerimeter(10,20)").Eval(ctx), 60);
}Part 7 — Reflection Context
The above example works well enough however if you have a lot of variables or functions it’s not a very elegant solution. Instead of hand coding all your variables and functions, .NET Reflection can be used to call the methods and properties of a C# object.
ReflectionContext does exactly this — it takes a target object and provides an IContext that will call the the methods and parameters of that object.
public class ReflectionContext : IContext
{
public ReflectionContext(object targetObject)
{
_targetObject = targetObject;
}
object _targetObject;
public double ResolveVariable(string name)
{
// Find property
var pi = _targetObject.GetType().GetProperty(name);
if (pi == null)
throw new InvalidDataException($"Unknown variable: '{name}'");
// Call the property
return (double)pi.GetValue(_targetObject);
}
public double CallFunction(string name, double[] arguments)
{
// Find method
var mi = _targetObject.GetType().GetMethod(name);
if (mi == null)
throw new InvalidDataException($"Unknown function: '{name}'");
// Convert double array to object array
var argObjs = arguments.Select(x => (object)x).ToArray();
// Call the method
return (double)mi.Invoke(_targetObject, argObjs);
}
}We now have a super easy way for expressions to call a library of C# code:
class MyLibrary
{
public MyLibrary()
{
pi = Math.PI;
}
public double pi { get; private set; }
public double r { get; set; }
public double rectArea(double width, double height)
{
return width * height;
}
public double rectPerimeter(double width, double height)
{
return (width + height) * 2;
}
}
[TestMethod]
public void Reflection()
{
// Create a library of helper function
var lib = new MyLibrary();
lib.r = 10;
// Create a context that uses the library
var ctx = new ReflectionContext(lib);
// Test
Assert.AreEqual(Parser.Parse("rectArea(10,20)").Eval(ctx), 200);
Assert.AreEqual(Parser.Parse("rectPerimeter(10,20)").Eval(ctx), 60);
Assert.AreEqual(Parser.Parse("2 * pi * r").Eval(ctx), 2 * Math.PI * 10);
}Taking it Further
We’ve now got a handy little expression engine. Here’s some ways you might like to extend it:
- Other Types — instead of working just with doubles add support for strings, bools and other types.
- Simplification — if you’re after a fast expression engine you could write code to walk the expression tree and simplify it.
- Bit-wise Operators— bit-wise and, or, xor etc…
- Comparison Operators — greather than, less than etc…
- Ternary Operator — “x < y ? 10 : 20”
- Conditional Operators —And (&&) and Or (||) and don’t forget about the short-circuit evaluation.
- Support for object members. eg: “rocket.y” and “rocket.launchIn(10)”
- Variable and Function scopes.
You could even use this as the basis for an interpreted language or as part of a HTML template engine.
The full source code for SimpleExpressionEngine is available here: